[CS231n] 03. Loss Functions and Optimization
업데이트:
Reference
-
Lecture 03 - ( Slide Link, ,Youtube Link )
1. Loss Functions
- 가장 좋은 가중치 행렬 $W$를 얻기위해 어떻게 트레이닝 데이터를 활용해야하나?
- 이를 위해서는 $W$가 어떤지를 평가할 수 있어야하고, 지금의 $W$가 얼마나 나쁜지를 정량적으로 말할 수 있어야함.
- 이를 위한 함수가 loss function
- 가장 괜찮은 $W$를 찾아나가는 과정이 optimization

- $L$ : dataset에서 각 N개의 샘플들의 Loss 들의 평균
- 위 함수는 컴퓨터 비전(CV)외에도 다양한 분야에서 사용
1) Multiclass SVM Loss
- binary SVM (Support Vector Machines)은 두가지의 class를 다루기 위한 알고리즘이었다면, multiclass SVM은 여러개의 클래스를 다룸
-
$L_i$를 구하려면 우선 true인 카테고리를 제외한 나머지 카테고리 Y의 합을 구해야함

- $S_{y_i}$ : training set의 $i$ 번째 이미지의 정답 클래스의 스코어
- $S_j$ : classfier의 출력으로 나온 예측된 스코어
- 예를 들어, $i$번째 이미지가 차였다면 차에 대한 스코어가 $S_{y_i}$, 고양이나 개구리에 대한 스코어가 $S_j$

- $L_i$ : 이 분류기가 얼마나 이상하게 분류를 했는가
- $L = (2.9 + 0 + 12.9) / 3 = 5.27$ 만큼 이상하게 분류를 함
- safety margin : 1은 뭔지? → 사실 1이라는 상수가 별로 중요한 숫자는 아님. 손실함수의 스코어의 절대적인 값이 중요한 것이 아니라 여러 스코어간의 상대적인 차이가 중요한 것.
- 즉, 정답 스코어가 다른 스코어에 비해 얼마나 더 큰 스코어를 가지고 있냐가 중요함.
- 결국에 1이라는 파라미터는 없어지고, W의 스케일에 의해 상쇄될 것
Q1. What happens to loss if car scores change a bit?
- Car score는 이미 다른 score들에 비해 많이 높음. 즉, 스코어를 조금 바꾼다 해도 서로 간의 간격(margin)은 유지될 것이고 loss는 계속해서 0일 것
Q2: what is the min/max possible loss?
- 최솟값은 0 (모든 class들에서 정답 스코어가 가장 크면 loss값은 0일 것)
- 손실함수가 hinge loss모양. 만약 정답 스코어가 엄청 작은 음수값이라면 loss는 무한대일 것(최댓값은 무한대)
Q3: At initialization W is small so all s ≈ 0. What is the loss?
- C-1 의 클래스를 순회함. 근데 비교하는 두 스코어가 거의 비슷하기 때문에 margin값과 유사한 1의 스코어를 얻게 될 것이고 이들이 쌓이다 보면 loss는 C-1이 됨
- 디버깅 전략,, training을 처음 시작할 때 loss가 C-1가 아니라면 버그가 있는 것 -> 수정을 해야함 !!
Q4: What if the sum was over all classes? (including $j = y_i$)
- 만약에 정답인 아이까지 다 하면 어떻게 되나? → loss가 1 늘어남.
- 실제로 정답 클래스만 빼고 계산하는 이유는 loss가 0이어야 아무것도 잃는 것이 없다고 해석할 수 있기 때문
Q5: What if we used mean instead of sum?
- 평균을 취한다는 건 스케일링을 하는 것일 뿐, 결과는 똑같음
Q6: What if we used
- 손실함수의 계산 자체가 달라짐. 이렇게 사용하기도 함.(장단점이 있음)
Q7 : Suppose that we found a W such that L = 0. Is this W unique?
- 여러개의 W가 생길 수도 있음. W에 scaling을 해도 비슷할 것
Code
def L_i_vectorized(X, y, W):
scores = W.dot(X)
margins = np.maximum(0, scores - scores[y] + 1)
margins[y] = 0 #정답 class만 0으로 만들어서 이를 무시
loss_i = np.sum(margins)
return loss_i
2) Regularization
Overfitting의 가능성
- training data에 꼭 맞는 W를 찾는게 좋은 것만은 아님,, → test data에 적용했을 때 괜찮은 분류기를 만드는 것이 목적이기 때문
- 아래의 예시에서 training data에 fit하게 파란색의 구불구불한 선으로 학습을 시켰는데, 실제 test데이터에서 원하는 선은 초록색의 선이라면 잘못 학습을 시킨 것!

-
따라서 이를 위해 **Regularization term**항을 추가!!
- Data Loss term : 분류기가 트레이닝 데이터에 fit되도록 함
- Regularization term : 모델이 조금 더 단순한 W를 선택하도록 도와줌 (overfitting을 방지하기 위한 term)
- $\lambda$ : regularization strength, hyper-parameter로서 우리가 학습 전에 설정을 해야함

L2 Regularization

- L2 Regularization 는 모든 x 의 요소가 골고루 영향을 미치기 원함 → w1보다 w2가 더 좋은 가중치라 판단
- 반면, L1 Regularization 은 w1가 w2보다 좋은 가중치라고 판단 (L1은 일반적으로 sparse한 solution을 선호함. w중 0의 값이 많을 수록 선호)
- “복잡하다” : (L1 = 0이 아닌 요소들이 많다), (L2 = W가 고르지 않다, 전체적으로 퍼져있다면 복잡하지 않은 것)
3) Softmax Classifier (Multinomial Logistic Regression)

- softmax func : 확률이기 때문에 0~1의 값을 가지고, 합치면 1이 됨
- 목표 : 정답 클래스에 해당하는 확률이 1에 가까워지도록 만드는 것 ⭐
-
- log를 쓰는 이유?
- 정답에 해당하는 확률값을 최대화시키는 것보다 확률값에 log를 취한 값을 최대화시키는 것이 편하기 때문에 log를 쓰는 것
-
loss function는 게산한 값이 얼마나 나쁜지를 나타내는 지표이므로 logg값에 마이너스를 붙임

Q1: What is the min/max possible loss $L_i$?
- min : 0 (log 1이 되는 것이 목표이므로, 완벽하게 분류를 했다면 Loss값은 0이 될 것)
- max : 무한대
- but, 컴퓨터에서 유한 정밀도를 가지고는 최댓값이나 최솟값을 가지지 못함
Q2: Usually at initialization W is small so all s ≈ 0. What is the loss?
- $log(C)$
SVM vs Softmax

- 정답 스코어가 충분히 높고, 다른 클래스 스코어가 충분히 낮다면 SVM입장에서는 매우 분류를 잘한 것!!
- 다만, softmax는 확률을 1로 만드는 것이 목표이기 때문에 최대한 정답 클래스에 확률을 몰아넣으려고 할 것이고 그 외의 클래스는 음의 무한대로 만들력 할 것
🧐 SVM과 Softmax는 어떻게 다른가?
SVM은 일정 선(margins)을 넘기만 하면 더이상 성능 개선에 신경쓰지 않지만,Softmax는 더더더 좋게 성능을 높이려고 함. 실제 딥러닝에서 이 손실함수 간의 성능차이는 크지 않음

2. Optimization
1) Random Search
- 임의로 샘플링한 W를 엄청 많이 모아두고 loss를 일일이 계산한 후에 어떤 W가 가장 좋은지를 살펴봄
- bad,,,,,,,,,,,,,,, 알고리즘…
bestloss = float("inf")
for num in xrange(1000):
W = np.random.rand(10, 3073) * 0.0001
loss = L(X_train, Y_train, W)
if loss < bestloss:
bestloss = loss
bestW = W
print 'in attempt %d the loss was %f, best $f' % (num, loss, bestloss)
scores = Wbest.dot(Xte_cols)
Yte_predict = np.argmax(scores, axis = 0)
np.mean(Yte_predict == Yte) #return 0.1555
- CIFA-10으로 실험을 했을 때 15.5%의 accuracy
- 최신 알고리즘의 성능이 95%라는 걸 생각하면 매우 안좋은 성능,,
2) Follow the slope



- 매우 안좋은 방법,,, 짱짱 느리기 때문에 !!!!🥲
- 엄청 크고 깊은 모델이라면 파라미터가 엄청 많기 때문에 학습 속도가 매우 느려짐
⭐ 수치적으로 풀지 말고, 해석적으로 풀기 !!
- 즉, W의 모든 원소를 살펴보면서 gradient를 구하지 않고, gradient를 나타내는 식을 찾은 후에 gradient dW를 계산하기 !!
⭐ In summary:
- Numerical gradient: approximate, slow, easy to write
- Analytic gradient: exact, fast, error-prone → In practice: Always use analytic gradient, but check implementation with numerical gradient. This is called a gradient check.
3) Gradient Descent ⭐️
- 엄청 크고 복잡한 신경망 알고리즘을 어떻게 학습시킬지에 대한 ⭐️핵심 아이디어⭐️
- W을 임의의 값으로 초기화한 후(random initialize), loss와 gradient를 계산
- 이후, 가중치를 gradient의 반대방향으로 업데이트 함 (back-propagation)
- step_size(learning rate) : 가장 중요한 hyper-parameter들 중 하나
# Vanilla Gradient Descent
while True :
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_grad
4) Stochastic Gradient Descent (SGD)
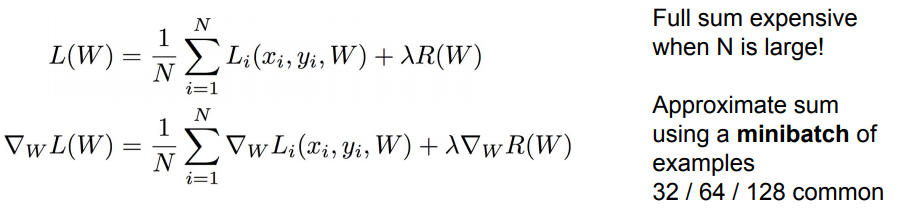
- imagenet에서 N은 130만개.. 이처럼 N이 아주 큰 경우에는 Loss를 계산하는 데에 엄청 오랜 시간이 걸림
- Loss : 각 데이터 Loss의 Gradient의 합
- 즉, gradient를 계산하려면 N번만큼 더 계산을 해야함
- 그래서 SGD의 방법을 씀 → Minibatch라는 작은 집합을 나눠서 계산
# Vanilla Minibatch Gradient Descent
while True :
data_batch = sample_training_data(data, 256)
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -step_size * weights_grad

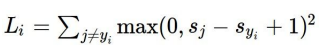


댓글남기기