[Paper Review] StyleGAN3: Alias-Free Generative Adversarial Networks 논문 리뷰

• Paper : Alias-Free Generative Adversarial Networks (NeurIPS 2021) (arxiv, code, project)

• 😎 StyleGAN Review Series
  • [Paper Review] StyleGAN : A Style-Based Generator Architecture for Generative Adversarial Networks 논문 분석
  • [Paper Review] StyleGAN2 : Analyzing and Improving the Image Quality of StyleGAN 논문 분석
  • [Paper Review] StyleGAN2-ADA #01: Training Generative Adversarial Networks with Limited Data 논문 분석
  • [Paper Review] StyleGAN2-ADA #02: Training Generative Adversarial Networks with Limited Data 코드 리뷰
• GAN-Zoos! (GAN 포스팅 모음집)

---

0. Abstract

• Probloem: 기존의 StyleGAN2은 texture sticking 이라는 문제를 가지고 있다. 이미지는 구조적으로 학습되어야 하는데(ex. 턱에 해당하는 위치에 수염이 있어야함), stylegan의 generator는 이미지의 각 특징들을 hierarchical 방식으로 학습하지 않고 고정된 픽셀 단위로 학습을 한다.
  • interpolation 영상을 보면, StyleGAN2의 결과는 턱 수염이 인물을 따라가지 않고, 픽셀 단위로 고정되어 있는 것을 확인할 수 있음.
• Cause: careless signal processing that causes aliasing in the generator network
• Problem Solving: hiearchical 하게 이미지를 합성할 수 있도록 alias-free 한 network 제안
  • translation이나 rotation에 대해 equivariance를 만족
  • video나 animation을 만들기에 적합

1. Introduction

figure1

• 기존의 StyleGAN generator: coarse, low-resolution feature에서 시작하여 upsampling하고, convolution으로 local하게 mixing하고, non-linear function을 거쳐 detail들을 찾아가는 방식으로 학습한다.
  • coarse feature들이 finer feature의 여부에 대해서는 조절을 하지만, 정확한 위치까지 control하지는 못함
  • 결과적으로, fine detail이 hiearchical하게 학습되는 것이 아니라 pixel coordinate에 고착화된 상태로 학습이 됨
• 이러한 texture sticking 문제는 fig1에서 확인할 수 있음
  • latent interpolation을 통해 자연스러운 transformation을 만들었을 때, 이 transformation이 hierarchy하게 조절되는 것이 아니라 각 feature들이 특정 pixel에 고착화되어 있음
• ⭐️ Our goal is an architecture that exhibits a more natural transformation hierarchy, where the exact sub-pixel position of each feature is exclusively inherited from the underlying coarse features.

1.1 The cause of the problem

현재 network가 이상적인 hierachical construction을 가지지 못하는 이유는 여러 가지가 있다.

1. image borders: stylegan은 image border가 spatial information을 줘서 generator가 texture sticking이 되도록 학습이 되고 있음 → (sol) image 를 좀 더 크게 잡은 다음에 나중에 crop하는 식으로 학습 (3.4.1)
2. per-pixel noise inputs: stylegan에서는 각 pixel마다 independant한 gaussian noise가 들어감. 우리는 pixel에 들어가는 transform에 따라 이미지가 다르게 생성되기를 원하기 때문에 translation과 independant한 noise를 넣어주면 안됨 → (sol) alias-free gan에서는 이를 제거 ! (3.3)
3. positional encoding (3.2)
4. aliasing ⭐️

저자들은 이 중에서 aliasing이 가장 critical한 issue라고 주장한다. network는 aliasing이 조금만 존재해도 이를 증폭하는 경향이 있어서 학습이 진행되면서 scale이 커질 수록 픽셀에 특정 texture가 고착되곤 한다.

🤔 Aliasing은 왜 발생하나?

1. non-ideal upsampling filters (ex. nearest, bilinear, strided conv): generator에서 upsampling을 하는 과정에서 low-path filtering을 하지 않았음. 즉 ideal하지 않은 upsampling filter때문에 원치 않은 high-frequency들이 계속 더해져서 aliasing이 일어나는 것 (sol in 3.4.1)
2. pointwise application nonlinearities such as ReLU: 예를 들어 음수일때 0으로 만들어주는 relu가 있으면 갑자기 값이 확 튀게 됨 (sol in 3.4.2)

또, 저자들은 이러한 aliasing에서 비롯되는 문제가 stylegan 뿐만 아니라 deep learning에서 전반적으로 발생한다고 보고하고 있다.

그렇다면, aliasing은 어떻게 해결할 수 있을까?

이론적으로 aliasing은 Nyquist-Shannon sampling theorem 로 해결된다. 저자들은 StyleGAN2의 Generator를 신호론적으로 분석하여 upsampling filter랑 pointwise nonlinearties에서 생기는 aliasing을 해결하고자 하였다.

(잡담 🥸) stylegan3는 위에 언급한 4가지의 문제를 해결함으로써 모델을 equivariance하게 만드는게 핵심인 논문이다. 왜 논문의 이름이 equivariance-gan가 아니라 alias-free gan인지에 대해 고민을 해봤는데, (4가지 문제 중 하나가 alias이니까..) 저자들이 주체적으로 해결한 문제가 aliasing이어서 인 것 같다.

1, 2, 3에 해당하는 문제들은 다른 논문들에서 문제제기를 하고 해결을 했다면, 4에 해당하는 aliasing 문제는 이 논문에서 처음으로 문제를 제기하고 해결을 했기 때문에 논문의 제목이 alias-free gan이 아닐까 추측한다.

그래서인지 1, 2, 3 문제의 해결책은 논문에서 불친절하게 설명되어있다. 1, 2, 3번 문제를 어떻게 해결했는지에 대해 자세하게 이해를 하려면 reference 논문을 읽어보고 이해할 필요가 있다.

---

1.2 Equivariance 의 의미

About translation equivariant in CNN

최근 image classification 연구에서는 CNN이 translation equivariant 하지 못했을 때의 문제점에 대해 많은 연구가 진행되고 있다. (CNN 자체는 equivariance해야지 Gloval average pooling 을 통과했을 때, final representation이 translation invariant하게 됨)

• 참고할만한 글
  • CNN과 이미지가 찰떡궁합인 이유
  • translation invariance 설명 및 정리

저자들은 CNN representation이 translation equivariant 하려면, CNN에서 나오는 feature map이 Nyquist frequency 를 넘어서는 빠른 패턴들을 가지면 안된다고 보고한다. 즉, aliasing이 발생하면 안된다.

Equivariance

우리는 2D plane상에서 어떤 operation $f$ 가 특정 transformation $t$ 에 대해 교환 법칙이 성립되면 equivariant 하다고 말한다.

\[\mathbf{t} \circ \mathbf{f}=\mathbf{f} \circ \mathbf{t}\]

🥸 본 논문은 이미지를 생성하기 위한 다양한 operation(ex, CNN, ReLU, Upsampling / Downsampling..)에서 Equivariance 해야한다고 계속해서 주장한다. Generator 모델을 Equivariance 하게 만드는 것이 논문의 핵심이다.

Equivarinace 해야한다는 것은 직관적으로 굉장히 당연한 개념이다.

예를 들어, 우리가 어떤 이미지를 회전시키고 싶을 때,

• latent code $z$ 로 부터 생성된 이미지를 회전시켰을 때랑
• 회전된 latent code $z$ 에서 생성된 이미지가

같다면, 이것이 바로 rotation에 대해 equivariant 한 것이다.

우리의 목표는 각각의 특징들을 hierarchical하게 학습하게 만드는 것이다.

따라서 각각의 layer들을 translation equivariant하게 만들어서 변형된 input으로 생성된 output이 일반 output을 변형한 것과 같도록 만든다면, 이미지의 각 특징들이 자연스럽게 hierarchical하게 학습될 것이다.

plus 😊

이전에 BDInvert라는 포스텍에서 나온 논문을 리뷰한 적이 있다. 이 논문은 stylegan의 generator에서 base code라는 중간 feature map $f$ 을 뽑아 변형시키면 output image도 변형된 상태로 생성된다는 논문이다.

• [Paper Review] BDInvert: GAN Inversion for Out-of-Range Images with Geometric Transformations 논문 리뷰

stylegan3의 equivaraiance가 input feature map을 변형시키면 생성된 output image도 동일하게 변형된다는 건데, 이 자체가 BDInvert의 컨셉과 비슷한 것 같다.

---

2. Equivariance via continuous signal interpretation

figure2

본 논문에서는 discrete domain와 continuous domain 사이를 자유롭게 넘나들 수 있도록 도와주는 operation에 대해 소개한다. (figure2 참고)

• sampling: continuous → discrete (by Dirac Comb)
• interpolation: discrete → continuous (by ideal interpolation filter)

figure3

• figure3: discrete ↔️ continuous domain 으로의 변환 과정에서 aliasing이 안생긴 채 신호를 sampling & interpolation 할 수 있도록 도와주는 이론 정리

• Nyquist-Shannon sampling Theorem (#01, #02)
  • 만약 신호가 대역제한(bandlimited)신호이고, 표본화 주파수가 신호의 대역의 두 배 이상이라면 표본으로부터 연속 시간 기저 대역 신호를 완전히 재구성할 수 있다.
  • 입력 신호의 최고 주파수 $f_{max}$ 의 2배 이상으로 모든 신호들을 균일하게 sampling 한다면, 원래 신호를 완벽하게 복원할 수 있다.
  • aliasing 현상: 아날로그 신호를 디지털 신호에 적용할 때, sampling 속도가 $2f_{max}$ 보다 작을 경우 아날로그 입력 신호에서 일부 최고 주파수 성분이 디지털 출력에 올바르게 출력되지 않는다. 따라서 이 디지털 신호를 다시금 아날로그 신호로 변환하고자 할 때, 원래 주파수에 없던 잘못된 주파수 성분이 나타난다.
  • ⭐️ 이 이론에 따라 신호를 sampling 하고 나면, sampling된 discrete feature map $Z(x)$ 이 나중에 continuous domain으로 복원하기 위한 충분한 정보를 가지고 있음
• Whittaker-Shannon interpolation Theorem
  • sinc interpolation
  • ideal band-limited inteporlation
  • ⭐️ discrete하게 sampling된 Dirac grid $Z(x)$ 와 ideal interpolation filter $\phi_{s}$ 를 convolution하고 나면, continuous 한 신호를 복원할 수 있음

\[z(\boldsymbol{x})=\left(\phi_{s} * Z\right)(\boldsymbol{x})\]

Discrete and continuous representations of network layers

또한, continuous domain과 discrete domain간의 변환이 자유로우려면 각각의 domain에서 행해지는 operation간의 변환도 자유로워야한다. (단, 이때 frequency가 bandlimit을 넘어서면 안됨)

\[\mathbf{f}(z)=\phi_{s^{\prime}} * \mathbf{F}\left(\mathrm{W}_{s} \odot z\right), \quad \mathbf{F}(Z)=\mathrm{W}_{s^{\prime}} \odot \mathbf{f}\left(\phi_{s} * Z\right)\]

• discrete domain
  • practical neural network는 discretely sampled feature map에서 동작
  • discrete feature map에서 convolution, nonlinearity와 같은 operation $F$ 은 다음과 같이 표현됨

\[Z' = F(Z)\]

• continuous domain

\[z' = f(z)\]

2.1 Equivariant network layers

⭐ 본 논문에서는 2가지 tranformation(translation, rotation) 과 전형적인 generator network의 4가지 operations(convolution, upsampling, downsampling, nonlinearity) 에 대해서 equivariant한지 확인한다.

또한, aliasing이 없으려면 nyquist sampling을 했을 때 이상한 high frequency가 없어야한다. 즉 low-path filtering이 output까지 유지되고 있는지를 확인해줘야한다.

2.1.1 Convolution

discrete domain

우선, discrete domain에서부터 살펴보자. discrete kernel $K$ 에서의 standard convolution은 다음과 같이 표현된다.

\[\mathbf{F}_{\text {conv }}(Z)=K * Z\]

continuous domain

discrete domain에서의 convolution 식을 continuous domain에서의 식으로 변환하면 다음과 같다.

\[\mathbf{f}_{\mathrm{conv}}(z)=\phi_{s} *\left(K *\left(\text { Ш }_{s} \odot z\right)\right)\]

(1) convolution은 commutativity 하므로 $\phi_{s} * K = K *\phi_{s}$

\[\phi_{s} *\left(K *\left(\text { Ш }_{s} \odot z\right)\right)=K *\left(\phi_{s} *\left(\text { Ш }_{s} \odot z\right)\right)\]

(2) ideal low path filter를 사용한다면, $z$ 를 dirac comb를 통해 sampling 한 후 ideal interpolation filter로 interpolation 하면 다시 $z$ 가 됨

\[\phi_{s} *(\text { Ш }_{s} \odot z) = z\] \[\mathbf{f}_{\mathrm{conv}}(z) = K *\left(\phi_{s} *\left(\text { Ш }_{s} \odot z\right)\right)=K * z\]

즉, convolution의 commutativity한 성질 (1) 때문에 translation equivariance 는 만족하며, convolution과정에서 새로운 frequency가 추가되거나 하지 않으므로 (2) domain간의 변환에서 추가적으로 aliasing 역시 생기지 않는다.

• translation 의 경우 convolution은 당연히 equivariance하다
• rotation equivariance의 경우에는, discrete kernel $K$ 가 radially symmetric해야하기 때문에 약간 주의할 필요가 있다. → 실제로 stylegan3 에서는 rotation equivariance를 만족시키기 위해 symmetric한 1x1 conv를 사용

---

2.1.2 Upsampling & Downsampling

Continuous domain에서의 Upsampling & Downsampling

continuous domain에서의 upsampling은 아무런 의미가 없다. (이미 infinite domain이니까)

\[f_{up}(z) = z\]

즉, translation or rotation을 하고 upsampling 한 것과 upsampling 하고 translation or rotation 하는 것이 동일하다 (equivariance)

Discrete domain에서의 Upsampling & Downsampling

그러나 discrete한 domain에서의 upsampling filter는 ideal 하지 않기 때문에 upsampling을 하는 과정에서 aliasing이 생기고, 이 때문에 등변성이 사라진다. 따라서 본 논문은 upsampling 과정에서 low path filtering을 하여 upsampling과 downsampling이 이상적으로 동작하는 것처럼 되게 한다. (→ equivariance !)

---

2.1.3 Nonlinearity

nonlinearity는 stylegan의 generator에서 유일하게 high-frequency를 학습할 수 있는 block이다. 그러나 non-linearity를 그냥 적용해버리면 의도치 않은 aliasing이 생길 수 있으므로 low-path filtering을 해서 새롭게 추가되는 정보의 양을 조절해야한다.

continuous domain에서는 ReLU가 pointwise operation이기 때문에 equivariance가 당연히 성립된다. 그러나 bandlimit constraint는 만족되지 않을 수도 있다.

즉, continuous domain에서 ReLU operation을 하고 나면 output에서 의도치 않은 high-frequncy가 생길 수 있다는 것이다. (aliasing)

논문에서는 이러한 aliasing을 제거하기 위해 non-linearity의 결과값에 low-path filtering을 해준다.

\[\mathbf{f}_{\sigma}(z)=\phi_{s} * \sigma(z) \quad \mathbf{F}_{\sigma}(Z)=\text { Ш }_{s} \odot\left(\phi_{s} * \sigma\left(\phi_{s} * Z\right)\right)\]

정리 ⭐️

• Generator가 low-resolution에서 시작하여 upsampling을 한 후
• non-linearity function을 통해 detail한 부분(high-frequency)을 만들어나가는데,
• 이때 생성되는 high-frequency 영역들을 low-path filter를 통해 cut-off 하면서
• high-frequency를 적절하게 학습하도록 함

---

3. Practical application to generator network

✍🏻 2절에서는 주요 operation에서 어떤 문제가 생기는지와 그것을 어떻게 해결하는지에 대해 소개하였다. 3절에서는 실질적인 문제들을 해결하기 위해 어떤 식으로 network를 바꿨는지에 대해 하나씩 설명한다.

3.1 StyleGAN2

Discriminator

• alias-free-gan에서는 stylegan2의 discriminator 구조를 유지 😊

figure4: stylegan2 architecture

Generator

1. mapping Network: initial, normally distributed latent code $z$ 를 intermediate latent code $w \sim \mathcal{W}$ 로 transform
2. synthesis network G: learned constant input 4x4x412 $Z_0$ 에서 N개의 layer를 거쳐 output image $Z_n = G(Z_0;w)$ 를 생성
   • N개의 layer: consisting of convolutions, nonlinearities, upsampling, and per-pixel noise
   • skip connection, mixing regularization, path length regularization 기법들도 도입

⭐️ Our goal is to make every layer of G equivariant w.r.t. the continuous signal, so that all finer details transform together with the coarser features of a local neighborhood

• 즉, transformation $t$ (translation & rotation)에 대해 equvariant 하도록 synthesis network의 operation $g$ 를 continuous 하게 만들어야함

\[\mathbf{g}\left(\mathbf{t}\left[z_{0}\right] ; \mathbf{w}\right)=\mathbf{t}\left[\mathbf{g}\left(z_{0} ; \mathbf{w}\right)\right]\]

Generator의 operation들을 equivariance하게 만드는 것이 이 논문의 핵심이다.

저자들은 각 operation이 얼마나 equivariance 한지 평가할 수 있는 방법도 함께 report 하였다.

• the peak signal-to-noise ratio (PSNR) in decibels (dB) between two sets of images
• EQ-T / EQ-R : 이 score가 높을 수록 translation / rotation에 대해 equivariance한 것
• 자세한 내용은 논문의 p5 를 참고

---

Result

figure5

3.2 Fourier features

이미지를 continuous하게 transformation(t&r) 하기 위해 learned constant input을 Fourier fearture로 변경하였다.

StyleGAN3에서는 fourier-feature-networks [56]와 Positional Encoding as Spatial Inductive Bias in GANs [66] 논문의 아이디어를 차용하여 learned constant input을 Fourier fearture로 대체하였다. 어떤 이점을 얻기 위해 Fourier Feature를 사용하였는지를 분석하고자 다음 논문([56, 66])을 간단하게 요약하였다.

3.2.1 Fourier Features Let Networks [56]

Paper: Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains (NeurIPS2020): project

• Fourier featuring란, coordinate space point를 frequency space로 embedding하는 function의 총칭이다.
• transformer 계열의 모델들에서는 feature의 위치 정보를 포함시키기 위해 sinusoidal function(fourier featuring function)을 사용하여 coordinate space에서 frequency space로의 embedding을 진행하는데, 이 역시 일종의 Positional Encoding이다 (참고 링크)
• 즉, Fourier Featuring을 통해 frequency domain으로 embedding하는 것 자체가 Positional Encoding의 효과를 준다.
• Fourier-Feature mapping function $\gamma$

\[\gamma(v)=\left[a_{1} \cos \left(2 \pi b_{1}^{T} v\right), a_{1} \sin \left(2 \pi b_{1}^{T} v\right), \ldots ., a_{m} \cos \left(2 \pi b_{m}^{T} v\right), a_{m} \sin \left(2 \pi b_{m}^{T} v\right)\right]^{T}\]

• Transformer등의 attention-based architecture들은 PE function으로 $\gamma$ 를 사용하며, 다음과 같이 정의된다.

\[a_{i}=1, b_{m}=10000^{m / d}, d: \text { dimension }\]

• 이 논문에서는 Fourier-Feature로 부터 PE 정보를 준 후, MLP를 통해 high-frequency를 학습해나가면서 고해상도의 이미지 생성을 학습한다.

---

3.2.2 Positional Encoding [66]

Paper: Positional Encoding as Spatial Inductive Bias in GANs (CVPR 2021): project, arxiv

figure-pe-1

• Problem: SinGAN, StyleGAN2과 같은 translation-invariant convolutional generator는 어떻게 spatial한 global structure를 학습하는가?
• Cause: zero padding - unbalanced spatial bias를 제공하여 위치 정보를 implicit하게 학습하도록 도움
• Contribution: 이 논문은 더 효과적인 spatial inductive bias를 제공하기 위해 (1) multi-scale training strage와 (2) explicit positional encoding 방식을 제안

translation-invariant convolutional generator가 정말로 위치에 invariant하다면, figure-pe-1 (b)의 결과처럼 이미지가 생성되어야 한다. 그러나 실제로는 figure-pe-1 (a) 처럼 이미지가 생성된다. ( = Generator가 어느정도 위치에 대한 정보를 학습한다는 것 )

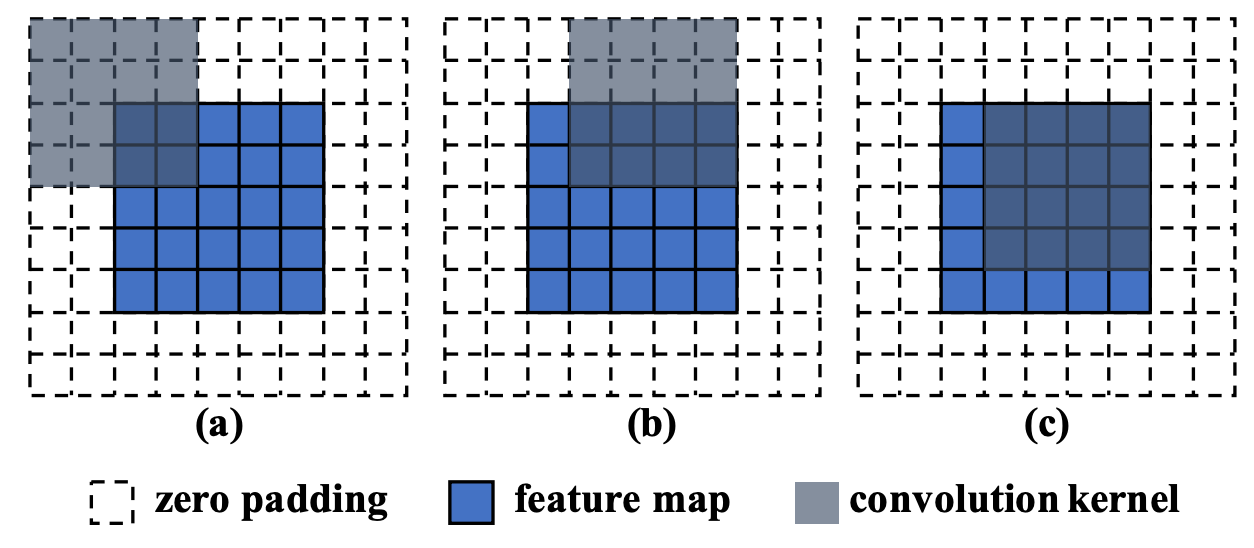
figure-pe-2

• 논문에서는 이러한 문제가 zero padding 때문이라고 설명한다. border 부분의 zero padding은 conv layer가 feature map의 distribution에서 location-aware bias를 학습하게 만들기 때문에, border 부분에서는 PE 정보를 학습하고 center로 갈수록 PE 정도를 학습하지 못하는 것이다.
• 즉, zero padding은 이미지 공간에 대해 unbalanced spatial bias를 주어 generator가 implicit하게 positional encoding 정보를 학습하도록 한다.

figure-pe-3

• top - standard StyleGAN2의 결과, bottom - padding-free StyleGAN2의 결과
• 오른쪽 세개의 그림 - learned constant input이 아니라 identical const input에서 생성된 이미지
• top: zero padding이 border 부분의 frozen structure를 학습하도록 하여 identical const input에서 생성된 이미지가 기존 이미지와 비슷한 border를 가짐
• bottom: zero padding을 제거하니 다양한 color와 pattern이 생김
• StyleGAN2 에서도 implicit positional encoding의 문제가 나타난다.

• (a): zero padding으로 인한 implicit spatial anchor는 border 부분에 대한 PE 정보를 학습하도록 도움
• (b): StyleGAN2의 generator는 4 x 4 x 512의 learned constant vector를 input으로 받는다. 이는 positional encoding의 정보를 explicit하게 주기는 하지만, 이로 인한 spatial inductive bias가 unclear하며 이미지 공간을 explicit하게 표현했다고 보기에도 부족함이 많다.
• (d): SPE (Sinusoidal Positional Encoding) 방식 = fourier featuring과 동일한 방식
  • nlp에서 positional encoding 을 주기 위해 자주 사용되는 방식이다.
  • 이를 이용하면 이미지에 대한 positional encoding 정보를 explicit하게 줄 수 있다.

---

정리 ⭐️

• 기존의 learned const input은 positional encoding 정보를 주기는 하지만, 좌표계가 좋지 않아 어떠한 방식으로 transformation이 작동되는지 알기 어려웠으며 이미지 공간을 explicit하게 표현했다고 하기에도 부족한 점이 많았다.
• stylegan2에서는 signal의 크기만을 encoding했다면, stylegan3에서는 새로운 coordinate system (SPE)을 도입하여 signal 뿐만 아니라 phase에 대한 정보도 잘 encoding하고자 하였다.

stylegan3는 Fourier Feature (in continous한 frequency domain)으로 input을 변경하여 infinit domain으로 확장하였고, 동시에 Postional Encoding 정보도 explicit하게 줄 수 있게 되었다.

• stylegan2의 constant learned input과 마찬가지로 학습과정에서는 이 입력값은 고정된다
• Fourier Feature를 도입하면 FID가 약간 개선됨: 5.14 ➡ 4.79 (figure5 (논문의 figure3))
• 또한, transformation(t&r) 가 가능해지는데, 대신 FID는 매우 떨어진다. (figure6)

• fourier feature를 사용함으로써 equivariance를 쉽게 측정할 수 있다. (figure5에서의 EQ-T, EQ-R)

• ✍🏻 참고할만한 링크
  • Position Encoding의 종류와 분석
  • gjghks950.log/Fourier Features Let Networks Learn High-Frequency Functions in Low Dimensional Domains Review
  • [논문 리뷰] Positional Encoding as Spatial Inductive Bias in GANs

---

3.2.3 Code

Fourier features는 stylegan3 의 코드에서 SyntehsisInput에 구현되어있다.

• SyntehsisInput block
  1. intermediate latent code $w$ 를 input으로 받아 affine 변환을 한 후,
  2. 이 값을 learned transformation: (1) 먼저 image를 rotation한 후 (2) translation (3) 마지막으로는 user-specified transform
  3. sampling grid를 만들어서 fourier feature로 변환

# Compute Fourier features.
x = (grids.unsqueeze(3) @ freqs.permute(0, 2, 1).unsqueeze(1).unsqueeze(2)).squeeze(3) # [batch, height, width, channel]
x = x + phases.unsqueeze(1).unsqueeze(2)
x = torch.sin(x * (np.pi * 2))
x = x * amplitudes.unsqueeze(1).unsqueeze(2)

---

3.2.4 Transformed Fourier Features(config H)

• 논문의 3.2 절에 해당

StyleGAN3 Generator의 layer들은 equivariant하기 때문에 unaligned dataset이나 임의로 변형시킨 dataset에 대해서도 잘 학습이 된다. (만약 intermediate feature $z_i$를 변형시키면 final image $z_N$ 도 변형되어 생성)

그러나 layer 자체에서 global하게 transformation 하기에는 layer의 capability가 작다. 따라서 Input Fourier Features 자체를 변형시키는 방식으로 생성되는 이미지도 transformation되도록 한다.

• learned affine layer를 통해 input Fourier Features 가 global translation or rotation 되도록 만듦
• SyntehsisInput code의 이 부분

# Apply learned transformation.
t = self.affine(w) # t = (r_c, r_s, t_x, t_y)
t = t / t[:, :2].norm(dim=1, keepdim=True) # t' = (r'_c, r'_s, t'_x, t'_y)
m_r = torch.eye(3, device=w.device).unsqueeze(0).repeat([w.shape[0], 1, 1]) # Inverse rotation wrt. resulting image.
m_r[:, 0, 0] = t[:, 0]  # r'_c
m_r[:, 0, 1] = -t[:, 1] # r'_s
m_r[:, 1, 0] = t[:, 1]  # r'_s
m_r[:, 1, 1] = t[:, 0]  # r'_c
m_t = torch.eye(3, device=w.device).unsqueeze(0).repeat([w.shape[0], 1, 1]) # Inverse translation wrt. resulting image.
m_t[:, 0, 2] = -t[:, 2] # t'_x
m_t[:, 1, 2] = -t[:, 3] # t'_y
transforms = m_r @ m_t @ transforms # First rotate resulting image, then translate, and finally apply user-specified transform.

# Transform frequencies.
phases = phases + (freqs @ transforms[:, :2, 2:]).squeeze(2)
freqs = freqs @ transforms[:, :2, :2]

Transformation Result

figure6

---

figure5

3.3 Baseline Simplification

(1) per-pixel noise inputs를 제거하였다.

• stylegan2에 삽입되는 per-pixel noise는 이미지의 세부적인 요소들을 독립적이게 학습하도록 만들기 때문에, 이미지가 hierarchical하게 학습되지 못한다.
• noise를 제거하면, figure5 (논문의 figure3)를 보면 FID가 그닥 개선되지는 않지만 훨씬 equivariance 해진다.

(2) StyleGAN2-ADA에서 처럼 the mapping network depth 를 줄임

(3) disable mixing regularization and path length regularization

(4) output skip connections 제거

• FID score를 높이기 위해 2,3,4를 했었지만, 모델을 단순화하기 위해 FID는 약간 포기하고 2,3,4를 제거하였다.

3.4 Step-by-step redesign motivated by continuous interpretation

3.4.1 Boundaries and Upsampling (config E)

Boundaries: 본 논문에서는 feature map을 무한한 공간으로 확장했다고 가정한다. 따라서 target canvas에 어느정도의 margin을 준 후, high-layer로 갈수록 이 확장된 canvas를 crop 하였다.

• border padding이 내부 이미지의 coordinate의 값을 어느정도 갖고 있기 때문에 border를 explicit하게 extension하는 과정이 필요하다.
• 실험 결과, 10-pixel margin 정도면 충분하여 이를 사용했다 한다.

Upsampling: 기존의 bilinear 2X upsampling filter를 windowed sinc filter로 대체하여 low-pass filtering도 함께 하도록 하였다.

• 참고✍🏻: windowed sinc filter
• $n=6$의 large Kaiser window : upsampling의 과정에서 output pixel은 6개의 input pixel에만 영향을 받고, downsampling의 과정에서 input pixel은 6개의 output pixel에만 영향을 줌
• figure5 (논문의 figure3): resampling filter를 작게 설정하면($n=4$) translation equivariance가 안좋아지고, 이를 크게 설정하면($n=8$) training 속도가 느려짐

3.4.2 Filtered nonlinearities (config F)

2.1.3 에서 ReLU가 당연히 equivariance는 만족하지만, bandlimit를 지키지 않으면 aliasing이 생길 수도 있다고 보고하였다. 따라서 non-linearity function을 지날 때 low-path filtering을 꼭 해야한다.

• 저자들은 upsample-leaky ReLU-downsample의 sequence가 CUDA kernel에서 효과적으로 연산되도록 최적화를 했다고 한다. (10배 빨라짐 + memory saving)
• upsampling + downsampling 정도는 실험결과 $m=2$ 면 충분하다고 한다.

3.4.3 Non-critical sampling (config G) & Flexible layer (config T)

Non-critical sampling (config G)

aliasing은 generator의 equivariance를 망치는 원인이기도 하다. 따라서 각각의 layer를 지날 때 aliasing이 생기지 않도록 해야한다.

• config G에서는 저해상도의 layer에서 aliasing이 안생기도록 cutoff frequency를 $f_{c}=s / 2-f_{h}$ 로 낮춤 !

Flexible layer (config T)

이렇게 aliasing을 없애는 것은 중요하다. 그러나 이미지를 학습할 때 상위 layer로 갈수록 detail을 학습하는 것도 중요하다. 즉, high-frequency도 적절히 학습을 해야하는데, low-path filtering을 너무 강하게 걸어주다보면 aliasing은 안생기겠지만 high-frequency (detail)가 학습되지 못한다.

• 따라서 config T에서는 layer를 flexible하게 조절한다.

정리하자면,

• 저해상도의 layer에서는 aliasing이 안생기도록 lower cutoff frequency를 통해 low-path filtering을 강하게 걸어주고
• 고해상도의 layer에서는 이미지의 detail을 학습하는게 중요하므로 flexible하게 조절하여 high-frequency를 학습하도록 한다.

3.4.4 Rotation equivariance (config R)

network를 rotation equivariant하게 변형하고자 할때에는 2가지를 변경한다.

1. 3x3 conv를 1x1 conv 로 변경. 대신 feature map의 수를 2배로 늘린다
2. sinc-based downsampling filter를 radially symmetric jinc-based filter로 변경
   • 학습과정에서 trainable parameter가 56% 줄어드는 효과
   • FID는 비슷하며 EQ-R은 약간 향상됨

4. Results

• 실험결과는 표 참고
• FID도 괜찮으며 equivarince도 좋다고 보고
• training 속도 개선 + 연산 최적화 진행
• unaligned image에 대해 실험했다는 점이 인상깊었다. unaligned image에 대해 projection 해봐야지 😉

Internal representations

fourier feature라는 새로운 좌표계에서 이미지 생성을 시작하기 때문에 signal뿐만 아니라 phase 정보도 encoding할 수 있게 되었고, positional encoding 정보도 explicit하게 줄 수 있게 되었다.

---

마치며..

오래전부터 읽기 시작한 논문이었는데, background를 하나씩 채우면서 읽다보니 완독하는데 시간이 걸린 논문이다 😂 그만큼 신호처리에 대한 배경지식이 많이 필요했던 논문이라 읽기 어려웠다.

모델 자체의 architecture가 혁신적으로 바뀐 건 없지만, stylegan2가 가지고 있었던 다양한 문제들을 여러 논문의 모델들의 아이디어를 통해 풀어나간점이 흥미로웠다. 또, NVIDIA가 슬슬 image를 넘어 video나 animation을 위한 모델을 만드려고 시도하는 것 같다는 인상을 받았다.

여러모로 흥미로웠던 논문이다. official 코드가 공개된 만큼 다양하게 실험을 해봐야겠다 😊

---

Reference

• gjghks950.log/Fourier Features Let Networks Learn High-Frequency Functions in Low Dimensional Domains Review
• PR-338 Alias-Free Generative Adversarial Networks (StyleGAN3)
• Alias-Free GAN [20210802, Ha Hyunwoo]