[Paper Review] STROTSS: Style Transfer by Relaxed Optimal Transport and Self-Similarity 간단한 논문 리뷰

• Paper: STROTSS: Style Transfer by Relaxed Optimal Transport and Self-Similarity (CVPR 2019): paper), project, code
• GAN-Zoos! (GAN 포스팅 모음집)

STROTSS

Feature Extraction

• ImageNet으로 학습된 VGG16 network 를 사용
• network $\Phi$ 에서 뽑아낸 feature activations: $\Phi(X)_{i}$
  • 각 feature map을 bi-linear upsampling해서 original image $X$ 와 spatial dimension을 맞춤: $\Phi(X){l_1} … \Phi(X){l_L}$
  • low level edge, color features 부터 mid-level texture features, high-level semantic feature까지 포함

Style Loss

(1) Relaxed EMD Loss

• $X^{(t)}$ 로부터 추출된 n개의 feature vectors: $A={A_{1}, \ldots, A_{n}}$
• style image $I_S$ 로부터 추출된 m개의 feature vectors: $B={B_{1}, \ldots, B_{m}}$
• EMD(Earth Movers Distance)를 사용

\[\begin{aligned}\operatorname{EMD}(A, B)=& \min _{T \geq 0} \sum_{i j} T_{i j} C_{i j} \\\text { s.t. } & \sum_{j} T_{i j}=1 / m \\& \sum_{i} T_{i j}=1 / n\end{aligned}\]

• $EMD(A,B)$ : A와 B사이의 거리가 얼마나 먼지를 계산
  • Wasserstein Distance와 유사
  • T: transport matrix
  • C: cost matrix
  • 이 distance는 효과적이지만 optimal T cost가 너무나도 커서 학습하기가 힘듦(GD에 사용하기 부적합, $O(max(m,n)^3)$)

⇒ 저자들은 Relaxed EMD를 제안하였다.

• 두 개의 auxiliary distances를 사용
• 기존의 EMD는 constraint가 두개였다면 (1/m, 1/n)
• 이 방식은 constraint가 하나

\[\begin{array}{lll}R_{A}(A, B) & =\min _{T \geq 0} \sum_{i j} T_{i j} C_{i j} \quad \text { s.t. } \quad \sum_{j} T_{i j}=1 / m \\R_{B}(A, B) & =\min _{T \geq 0} \sum_{i j} T_{i j} C_{i j} \quad \text { s.t. } \quad \sum_{i} T_{i j}=1 / n\end{array}\]

• 최종 relaxed earth movers distance

  \[\ell_{r}=R E M D(A, B)=\max (R_{A}(A, B), R_{B}(A, B))\] \[\ell_{r}=\max (\frac{1}{n} \sum_{i} \min _{j} C_{i j}, \frac{1}{m} \sum_{j} \min _{i} C_{i j})\]

  • transport의 cost인 matrix $C$ 은 두 feature vector 사이의 cosince distance로 계산

    \[C_{i j}=D_{\cos }(A_{i}, B_{j})=1-\frac{A_{i} \cdot B_{j}}{\|A_{i}\|\|B_{j}\|}\]
    • 저자들은 feature vector대신 Euclidean distance를 사용하여 이미지간의 거리를 계산하기도 해봤지만, 결과가 더 안좋았다고 한다.

(2) moment matching loss

Relaxed EMD loss는 source image의 structural 정보를 target image로 전달하도록 도와주지만, feature vector의 크기는 무시한채 cosine distance를 구하기 때문에 output image에 visual artifact가 생길 수도 있다. ⇒ 저자들은 moment matching loss를 추가!

\[\ell_{m}=\frac{1}{d}\|\mu_{A}-\mu_{B}\|_{1}+\frac{1}{d^{2}}\|\Sigma_{A}-\Sigma_{B}\|_{1}\]

• moment matching loss에 관해서는 다음 논문을 참고

(3) color matching loss, $l_p$

output image와 style image가 비슷한 color palette를 가지도록 강제

• $X^{(t)}$와 style image $I_S$ 간의 pixel colors간의 Relaxed EMD 를 계산하였다고 하며,
• 이때는 Euclidean distance를 ground metric으로 사용했다고 한다
• 또한, 이미지를 RGB가 아닌 다른 색공간으로 변환하여 학습을 했더니 더 좋은 성능을 냈다고 한다.
  • 코드 보니까 YUV 색공간인듯?

Content Loss

이미지의 semantics나 spatial layout은 유지하지만, $X^{(t)}$의 pixel value가 $I_c$ 의 pixel value와 다를 수 있도록 보장해주는 term

• 어떤 coordinate에서 추출된 feature vector의 normalized cos distance를 사용하기 때문에 content image와 output image간의 일정한 거리가 유지될 수 있다.

• local self-similarity descriptor를 사용해서 robust하게 pattern을 인식

\[\mathcal{L}_{\text {content }}(X, C)=\frac{1}{n^{2}} \sum_{i, j}|\frac{D_{i j}^{X}}{\sum_{i} D_{i j}^{X}}-\frac{D_{i j}^{I_{C}}}{\sum_{i} D_{i j}^{I_{C}}}|\]

• $D^X$ : $X^{(t)}$에서 추출된 모든 feature vectors간의 pair-wise cosine distance
• $D^{I_c}$ : by content image

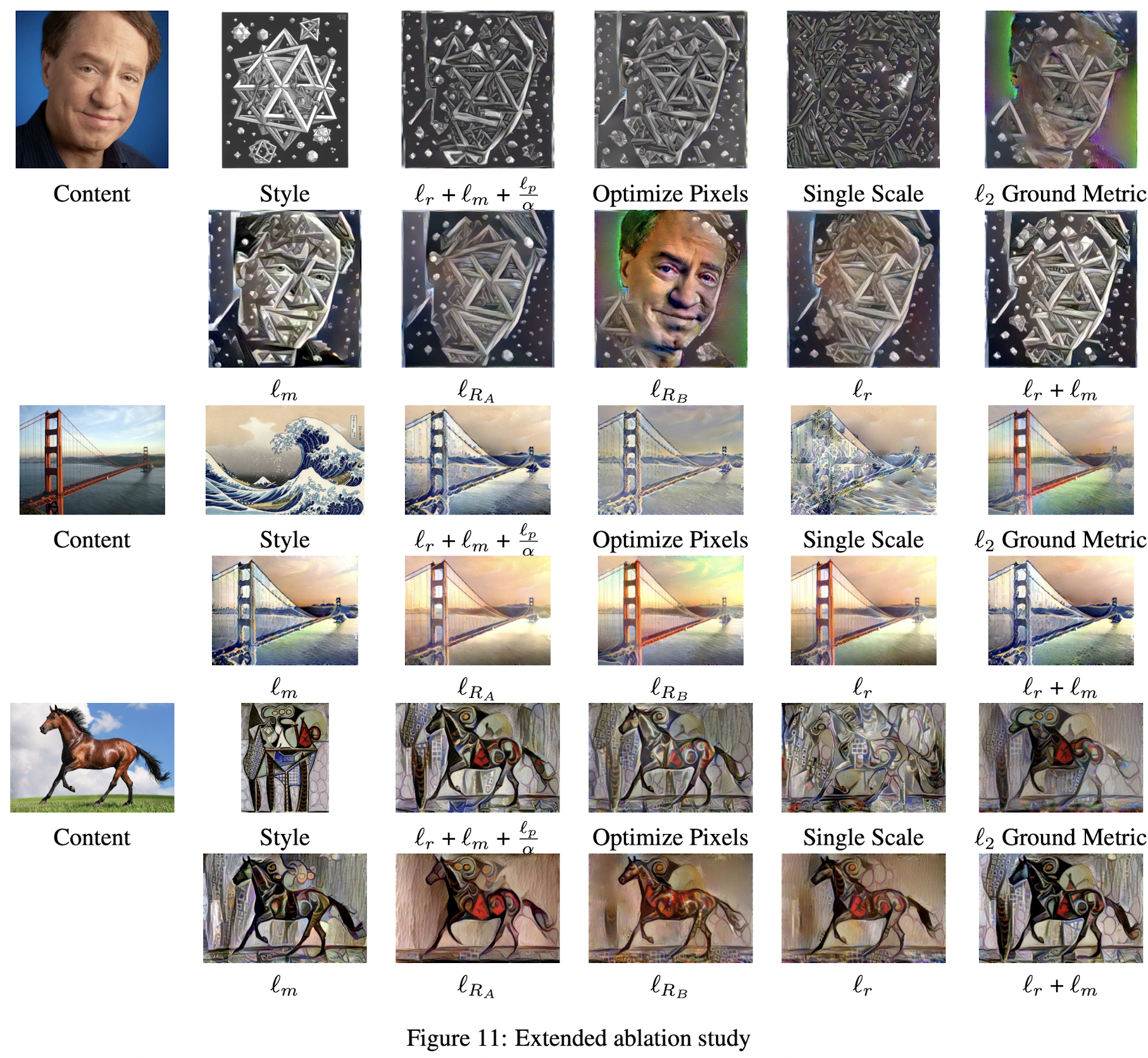
• moment matching loss $l_m$
  • 이 Loss만을 적용하면 style transfer는 잘하지만, style image의 large structure를 잃어버림
• the Relaxed Earth Movers Distance $l_r$
  • $l_R_A$ 와 $l_R_B$ 모두를 적용한 $l_r$ 의 결과가 가장 좋음
• color pallete matching loss $l_p$