Jihye Back

Jihye Back

꿈꾸는 꼬마 개발자 👩🏻‍💻 (Interested In GenAI)

Computer Graphics #02. Coordinate Space & Transformations

업데이트:

About Computer Graphics..

Geometry, rendering, animation, imaging, Materials & lighting, VR/AR, mobile GPU, deep learning

  • 김영민 교수님의 컴퓨터 그래픽스 수업을 듣고 요약한 글입니다.

3. Coordinate Space & Transformations (1)

3.1 Transformation

linear transformation

linear transformation

  • linear transformation
    • cheap to compute
\[f(\mathbf{x}+\mathbf{y})=f(\mathbf{x})+f(\mathbf{y})\] \[f(a \mathbf{x})=a f(\mathbf{x})\]
scale
rotation
reflection shear
  • scale과 rotation, reflection, shear는 linear transformation

translation

translation
  • translation은 linear transformation가 아님 !
    • affine transformation: linear transformation + translation
    • scaling하고 translation한 것과 translation하고 scaling하는 건 다름 => linear transformation X

Summary

3.2 Matrix multiplication

linear transformation

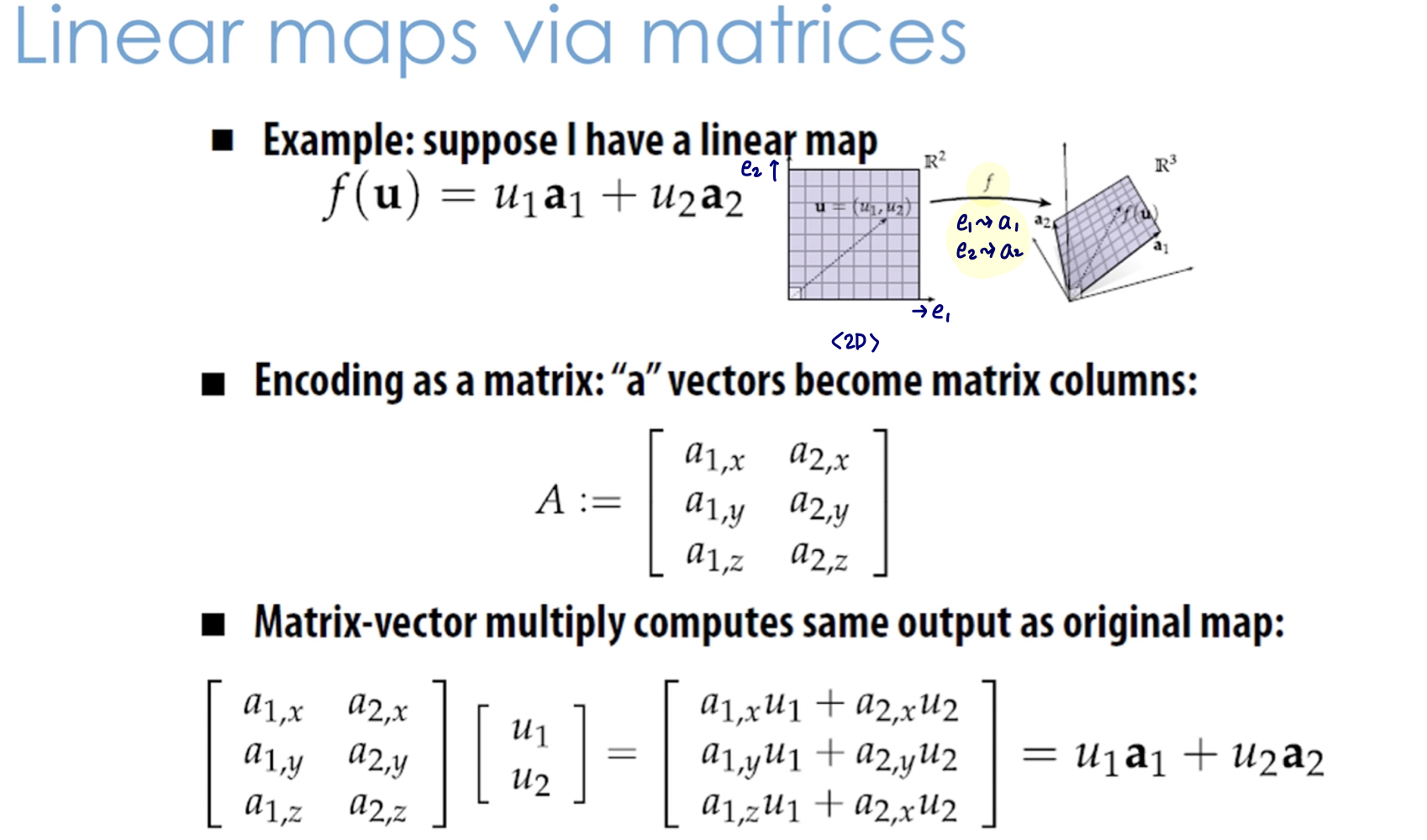
Homogenous coordinate

  • Homogenous coordinate: 2D points를 3 value로 표현
    • 3번째 extra coordinate로 나머지 2D coordinate를 나눠주면 다시 2D로 표현 가능

🧐 Homogenous Coordinate를 왜 사용할까?

우리는 Homogenous Coordinate을 사용함으로써 translation이나 perspective projection과 같은 non-linear transformation을 matrix 연산이 가능한 linear transformation으로 바꿀 수 있다. 대신 차원이 하나 늘어난다.

Scaling & Rotation

Translation

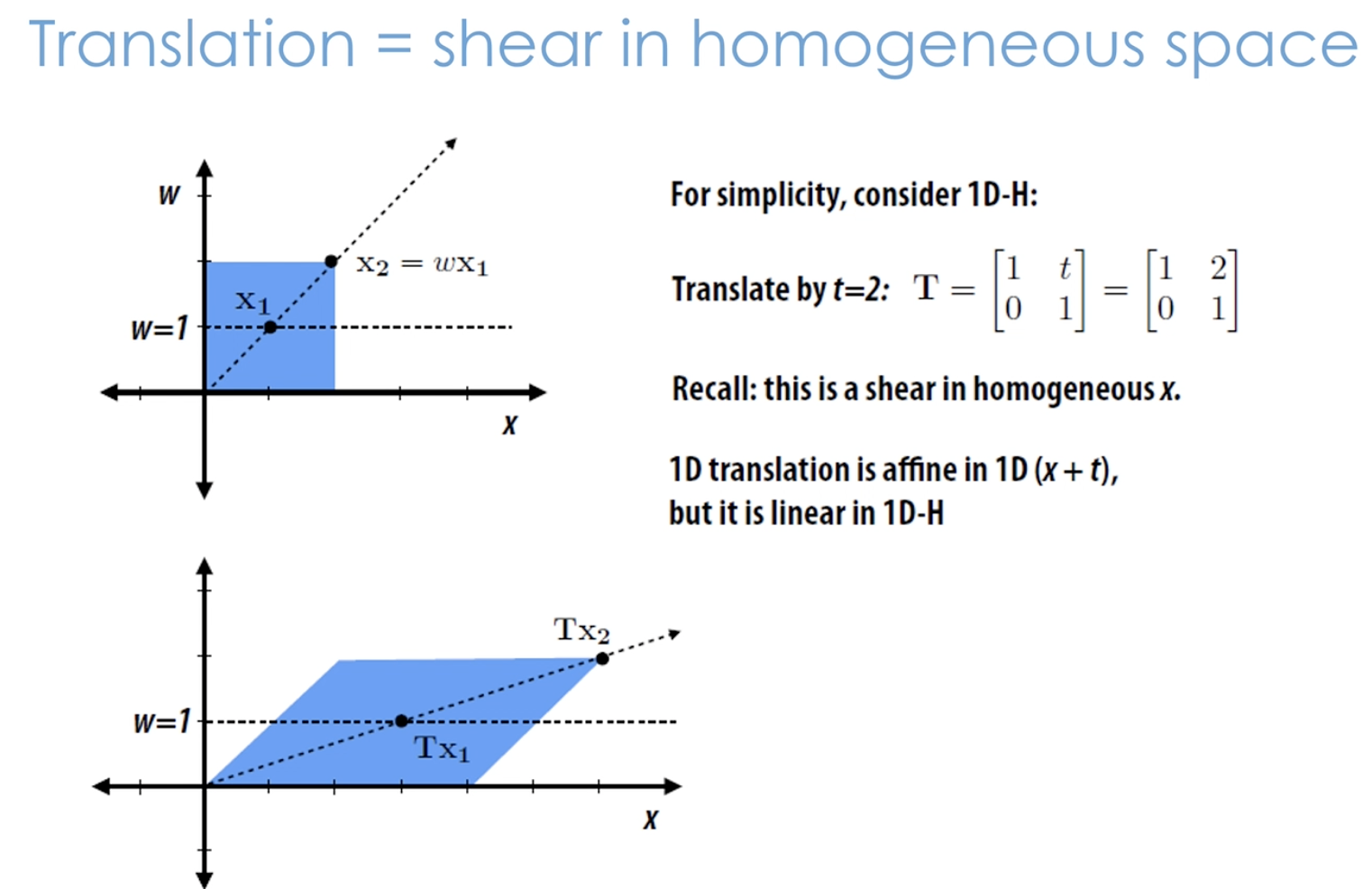
homogenous coordinate를 사용함으로써 translation을 linear transformation으로 볼 수 있음 !

  • 2D-homogenous space에서는 translation이 shear transformation 처럼 보임
  • 2D-H points 에서 $w=0$ 이면 2D vector가 됨 (infinite니까)
    • vector는 translation의 영향을 받지 않음

2D transformation in 2D-H

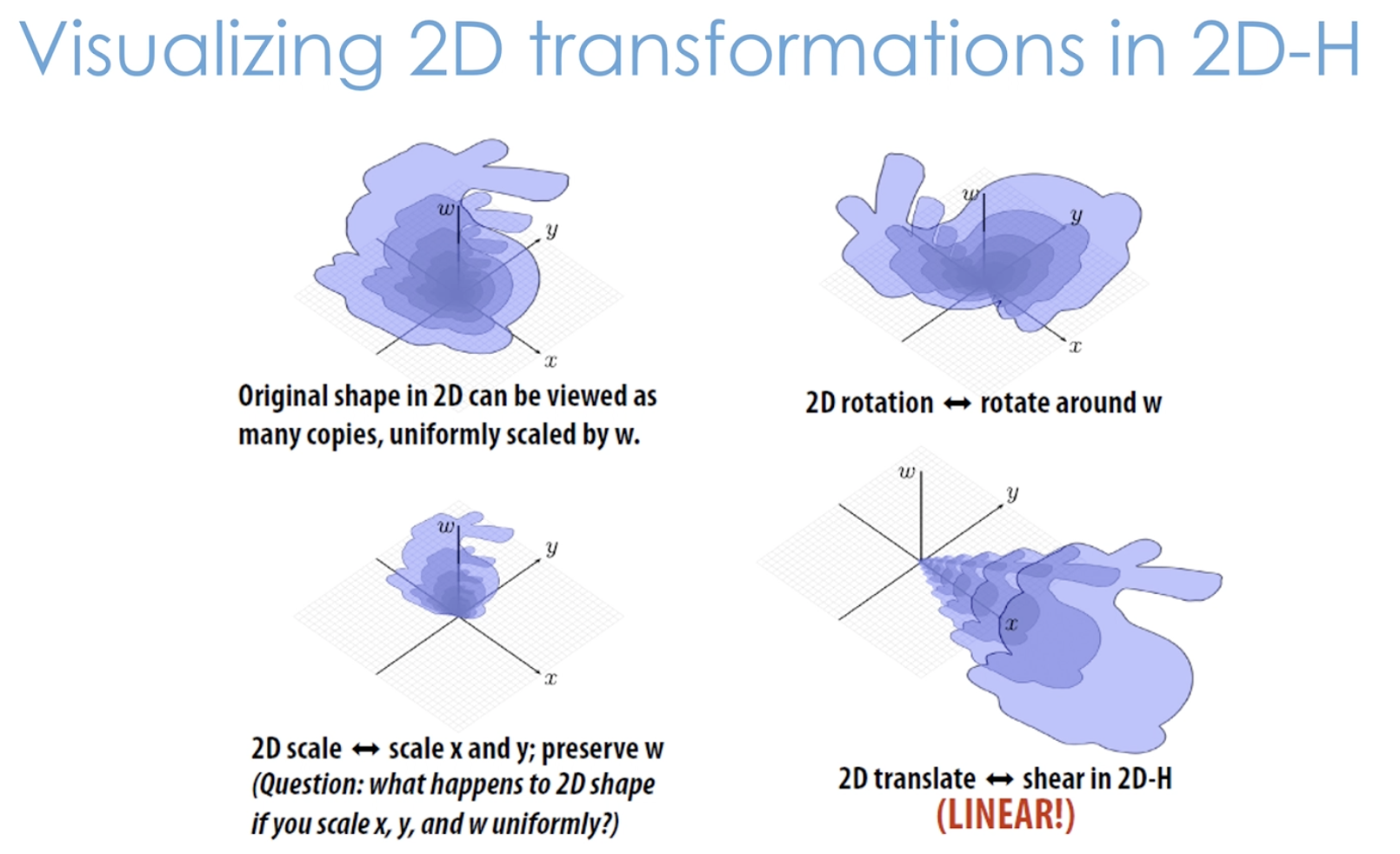
3D transformation in 3D-H

  • 3D-H 역시 마찬가지, 4x4 matrix로 표현됨
  • openGL이나 GPU는 4x4 matrix를 잘하도록 최적화가 되어있음
  • 3D에서는 rotation을 조심할 필요가 있음. 2D에서는 rotation 순서가 중요하지 않았지만, 3D에서는 중요
    • eular angle: Gimbal lock 문제가 생길 수 있음
    • 3D rotation에는 Axis-angle rotation이나 Quaternions 등의 방식을 사용

3.3 Chain

  • Transformation은 물체를 옮겼다고 생각할 수도 있지만, coordinate system이 바꼈다고 생각할 수도 있음
  • World coord에서 View coord으로 옮길 때는 rotation과 translation을 통해 coordinate를 바꿔줌

사람을 만들 때 hierarchical하게 그룹을 져서 만듦

4. Coordinate Space & Transformations (2)

4.1 Transformation

Homogenous Coordinate

  • N-dim의 coordinate가 있을 때 이를 N+1로 표현하는 것
  • 2D 데카르트 좌표계(Cartesian coordinate) $(X, Y)$ → 2D Homogeneous coordinate $(x, y, w)$
  • Why homogeneous?
    • scale invarient하기 때문
    • $(1a, 2a, 3a) \rightarrow (1/3, 2/3)$
    • $(0,0,0)$은 표현이 안됨
    • 원점을 제외하고 정의한 2D projective space $P^2 = R^3 - (0,0,0)$

2D transformatioin

  • Translation: 물체가 모양을 유지하며 움직이는 거
  • Euclidean: Translation + Rotation, 모양은 그대로
  • Similarity: Translation + Rotation + Uniform scaling
  • Affine: 물체의 모양이 약간 찌그러짐
  • Projective: 길이의 비율이 변함

4.2 Perspective Projection

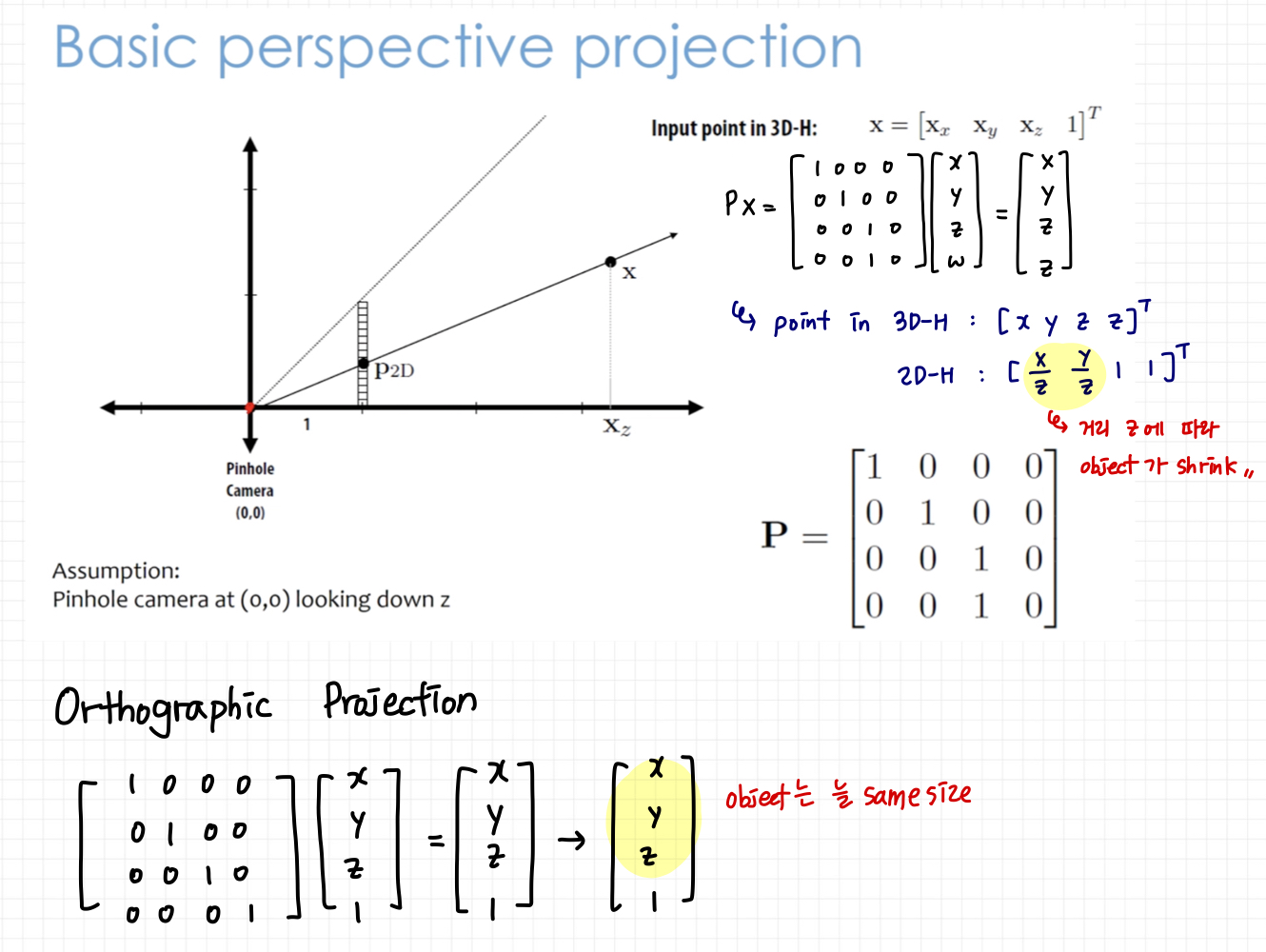
View frustum

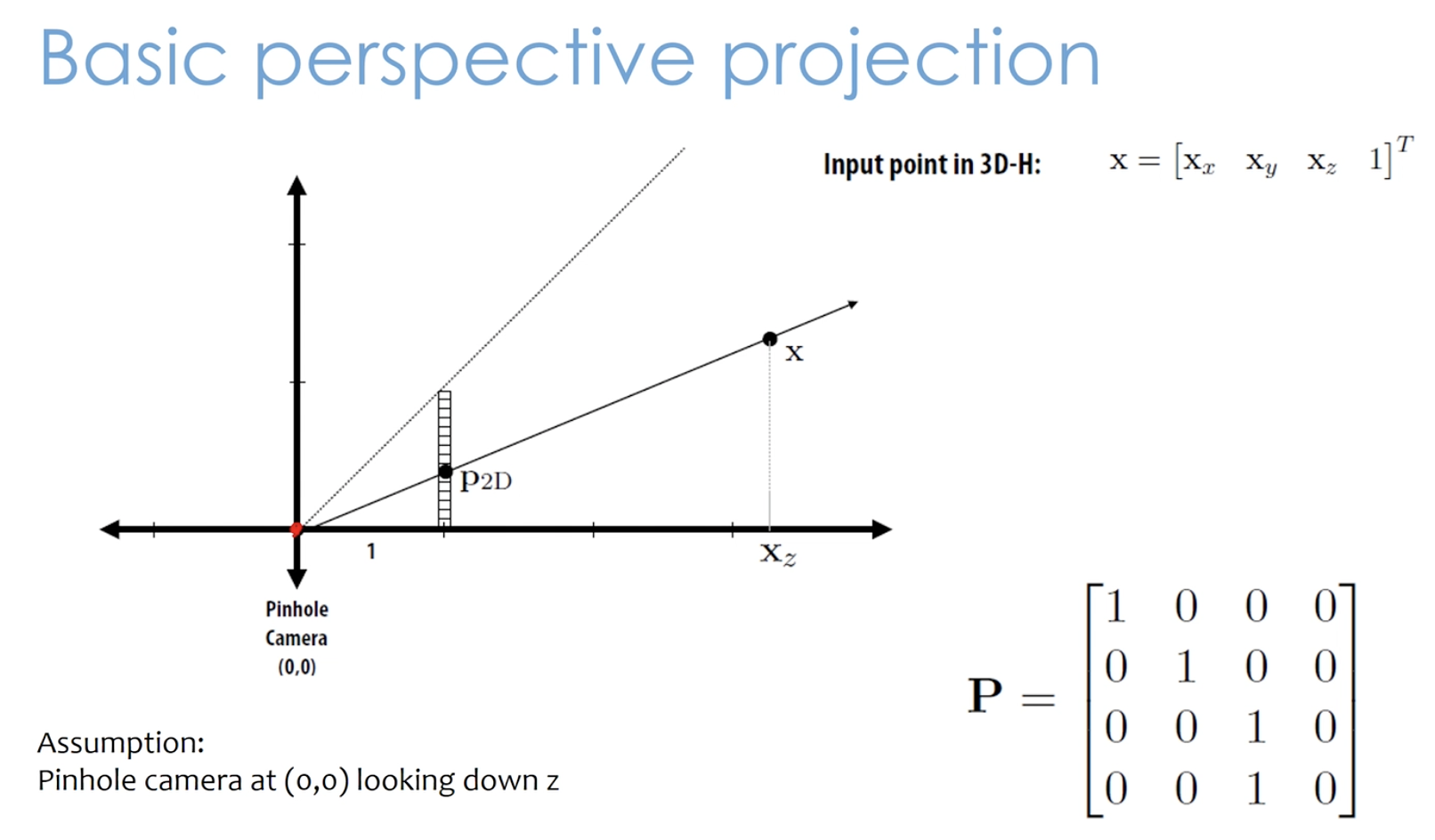
  • 카메라에서 볼 수 있는 영역

Clipping

  • 카메라에서 안보이는 부분에 해당하는 삼각형은 버리는 것
  • clipping을 하는 과정에서 사용하는 computation이 많아지면 (각각의 물체들이 Inside인지 outside인지 계산하는데 드는 cost) 오히려 clipping을 해서 얻는 이점이 적어지므로 여러가지 choice를 하게 됨

near/far plane clipping

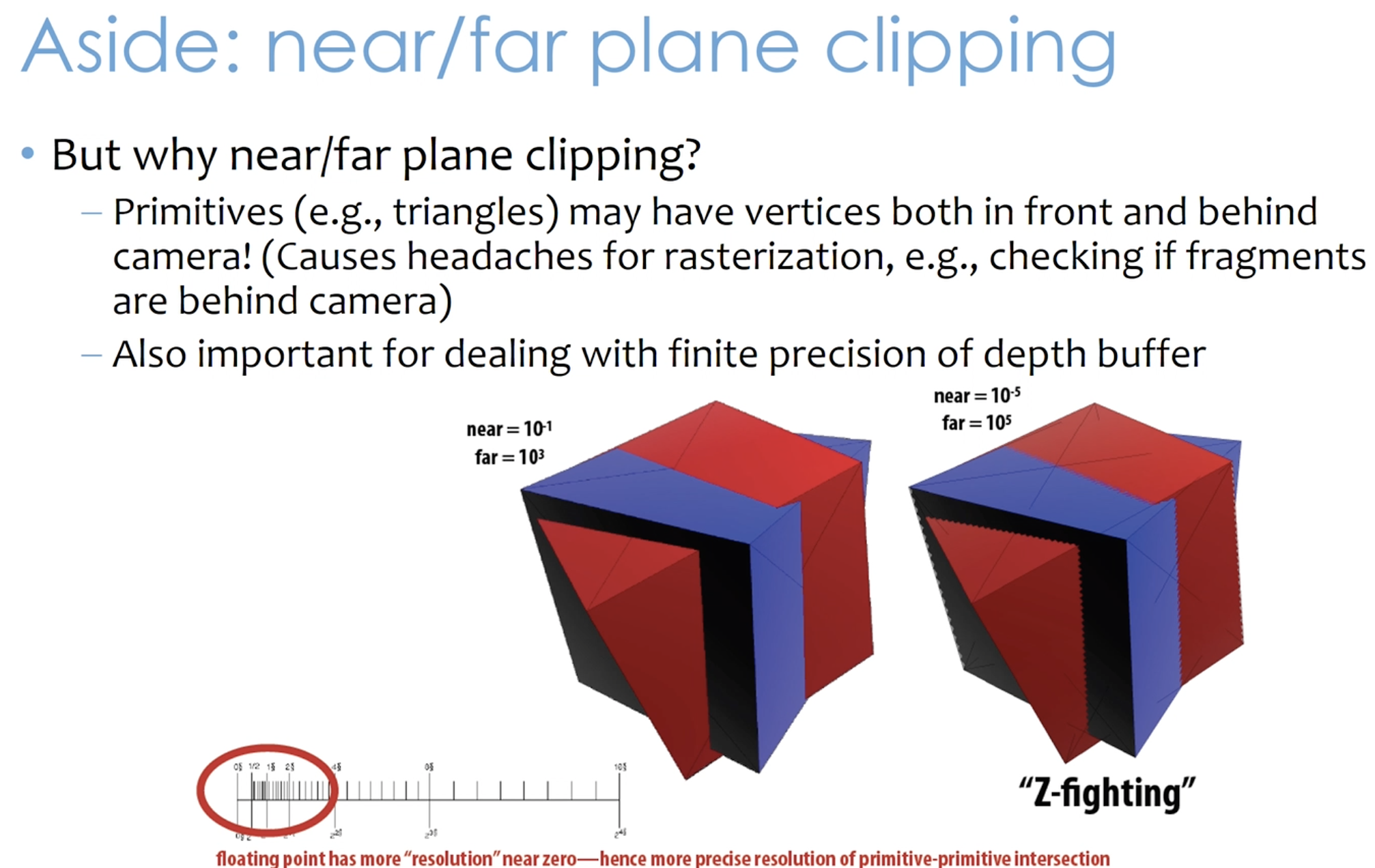
  • 어떤 물체가 너무 가까이에 있거나 너무 멀리 있으면 보이지 않음 ➡ 애초에 너무 가깝거나 먼 영역에 대해서는 미리 clipping

frustum to normalized cube

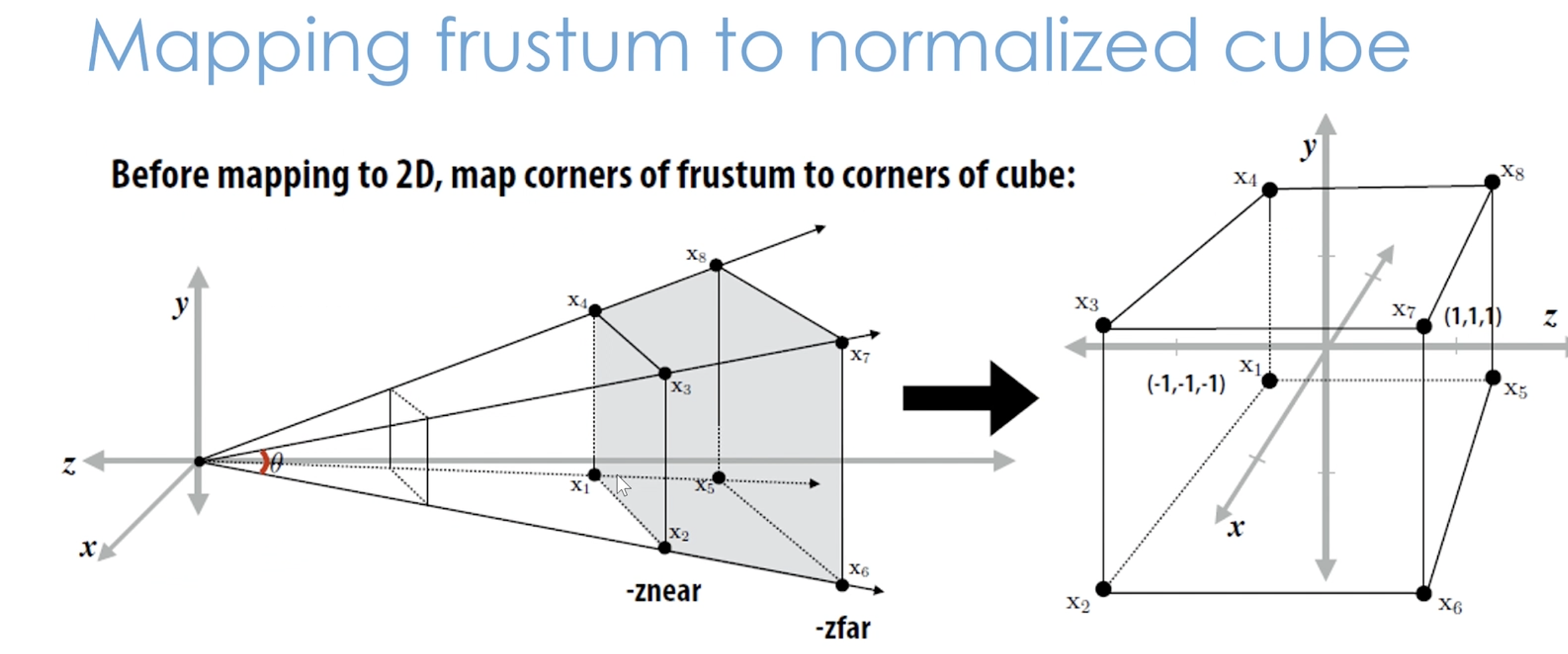
  • ㅎ사다리꼴 모양의 viewing frustum을 계산하기 편한 normalized cube로 옮기면 clipping을 더 간단하게 할 수 있음
    • [-1, 1] 의 outside 영역에 있는건 버리면 되니까
  • 원점에 가까운 경우에는 near clipping을 함으로써 precision issue를 피할 수 있음
  • 이렇게 nomarlized cube로 옮기는 거를 NDC(Normarlized Device Coordinate)라고 부름

Clipping in NDC(Normarlized Device Coordinate)

perspective transform

4.3 Rotations in 3D

Eular angle

  • $(x, y, z)$, 세 축으로 각각 얼마나 돌아갔는지를 표시하는 방법
    • 3축은 orthogonal 해야하는데, 여러가지 rotation에 따라 coordinate system이 변화하게 되면서 축간의 independence가 보장이 안될 때도 있음
  • Gimbal lock 문제가 생길 수도
Eular angle Gimbal lock

3D rotation group

3D rotation은 Special orthogonal group이자 lie group !

  • Euclidean distance(isometry)와 orientation(handedness of space)를 보존하지만, 순서를 바꿀 수는 없음
  • Group: 어떤 set $G$ 과 operation이 group 관계를 형성하려면 네가지 조건을 만족해야함
    1. Closure
    2. Associativity
    3. Identity element
    4. Inverse element
    • 예를 들어, 정수와 덧셈은 그룹임
  • Orthogonal Group: Euclidean space에서 길이가 바뀌지 않은 transformation들 (distance-preserving transformations)
    • transformation을 matrix로 표현했을 때, 해당 행렬이 n x n의 orthogonal matrices 이면, orthogonal transformation이 되는 것
    • Special orthogonal group $SO(n)$ : Orthogonal Group에서도 orthogonal matrices의 determinant가 1인 그룹

  • Lie Group: 미분이 가능한 differential manifold에 존재하는 operation

  • 참고할만한 글

Axis/Angle

Rodriquez’s formula

  • $\theta$ 가 작으면 $sin \theta$ 를 $\theta$ 로 근사할 수 있으므로 linear 하게 만들 수 있음

Exponential Twist

  • 위의 식을 다음과 같이도 유도할 수 있음

Reference

댓글남기기

참고